算法日记-LeetCode-931-下降路径最小和

2023-07-13

字数统计: 721字 | 阅读时长≈ 3分

算法日记-LeetCode-931.下降路径最小和

题目大意

给定一个n x n的矩阵 matrix，求出通过 matrix 的下降路径 的最小和 。

下降路径：从第一行中的任意元素开始往下，往下的过程中可以选择左下，正下，右下方的元素，即(i, j) 可以选择(i + 1, j - 1)，(i + 1, j)，(i + 1, j + 1)作为下一个元素。

示例

输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13

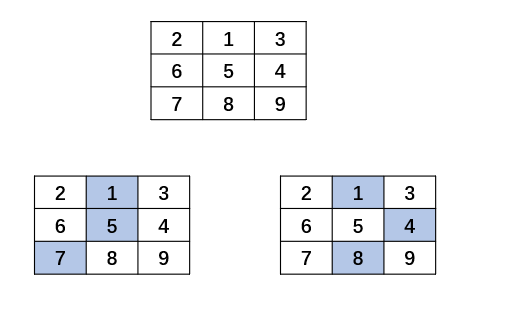
解题思路

这题是dp问题，也就是动态规划类的问题，我们需要找出状态转移方程。

根据题意，我们知道，我们从上往下走，可以从当前行元素，选择下一行中的特定三个值。

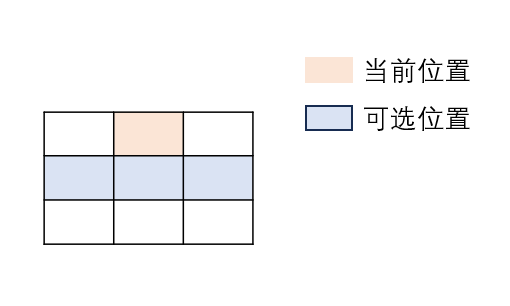
通过dp数组记录答案，dp[i][j]表示的是，从第一行到(i,j)位置的下降路径最小和，即dp数组中的每一个元素都是对应位置所求的答案。最后我们只要在最后一行，即dp[n - 1]中，找到最小值即可。

dp[i][j]的值，是martix[i][j]与上一行中三个相关位置的值，依赖关系如下：

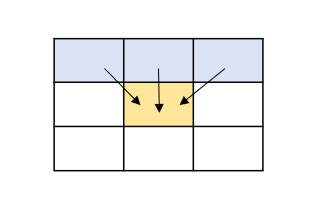
所以可以得到转移方程

dp[i][j] = martix[i][j] + min(dp[i - 1][j-1], dp[i - 1][j], dp[i - 1][j + 1])

即矩阵中的当前值，和dp数组中，可能到达给位置的最小值的和

需要注意边界，dp[i][0]，dp[i][n - 1]，这两个位置一个在最左边，一个在最右边，只与上一行中的两个值有关。

代码如下

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        int[][] dp = new int[n][n];
        for (int i = 0; i < n; i++) {
            dp[0][i] = matrix[0][i];
        }
        if (n == 1) {
            return dp[0][0];
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (j == 0) {
                    dp[i][j] = matrix[i][j] + Math.min(dp[i - 1][j], dp[i - 1][j + 1]);
                } else if (j == n - 1) {
                    dp[i][j] = matrix[i][j] + Math.min(dp[i - 1][j - 1], dp[i - 1][j]);
                } else {
                    dp[i][j] = matrix[i][j] + Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]);
                }
            }
        }
        int min = dp[n - 1][0];
        for (int i = 1; i < n; i++) {
            min = Math.min(min, dp[n - 1][i]);
        }
        // int min = Arrays.stream(dp[n - 1]).min().getAsInt();
        return min;
    }
}

0ms范例

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        int[] dp = new int[n];
        System.arraycopy(matrix[0], 0, dp, 0, n);
        dp = dfs(matrix, dp, 1, n);
        int res = Integer.MAX_VALUE;
        for (int j = 0; j < n; ++j) {
            res = Math.min(res, dp[j]);
        }

        return res;
    }

    private int[] dfs(int[][] matrix, int[] dp, int depth, int n) {
        if (depth == n) {
            return dp;
        }

        int[] nextDp = new int[n];
        for (int i = 0; i < n; ++i) {
            int cur = dp[i];
            if (i > 0) cur = Math.min(cur, dp[i - 1]);
            if (i < n - 1) cur = Math.min(cur, dp[i + 1]);
            nextDp[i] = cur + matrix[depth][i];
        }

        return dfs(matrix, nextDp, depth + 1, n);
    }
}

本文作者： Naskete
本文链接： https://Naskete.github.io/2023/07/13/algorithm/算法日记-LeetCode-931.下降路径最小和/
版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！